Prozentualer Unterschied berechnen: Formel, Beispiele & Anwendung

Was ist der prozentuale Unterschied?

Der prozentuale Unterschied beschreibt, um wie viel Prozent sich zwei Werte voneinander unterscheiden. Er gibt an, wie groß die Veränderung im Verhältnis zum ursprünglichen Wert ist. Im Gegensatz zum absoluten Unterschied, der einfach die Differenz zwischen zwei Zahlen misst, berücksichtigt der prozentuale Unterschied die Ausgangsgröße — und stellt sie ins Verhältnis.

In der Praxis wird der prozentuale Unterschied genutzt, um Größen fair miteinander zu vergleichen, unabhängig davon, wie groß die Werte selbst sind. Typische Beispiele sind Preisänderungen im Handel, Umsatzentwicklungen in Unternehmen oder Veränderungen in statistischen Zahlen.

Definition und Bedeutung

Mathematisch ausgedrückt, vergleicht der prozentuale Unterschied die Veränderung eines Wertes im Verhältnis zum ursprünglichen Wert. Das Ergebnis wird immer in Prozent angegeben, sodass unterschiedliche Situationen leichter vergleichbar sind.

Beispiel:
Wenn ein Produkt früher 80 € kostete und jetzt 100 €, beträgt der absolute Unterschied 20 €. Der prozentuale Unterschied hingegen zeigt: Der Preis ist um 25 % gestiegen.

Unterschied zwischen absoluter und prozentualer Differenz

• Absoluter Unterschied → Reine Differenz: neuer Wert minus alter Wert.
  
• Prozentualer Unterschied → Verhältnis der Differenz zum ursprünglichen Wert, ausgedrückt in Prozent.
  

Beispiel:

• Alter Preis: 80 €
  
• Neuer Preis: 100 €
  
• Absoluter Unterschied = 100 € – 80 € = 20 €
  
• Prozentualer Unterschied = (20 € ÷ 80 €) × 100 = 25 %
  

→ Während der absolute Unterschied 20 € beträgt, zeigt der prozentuale Unterschied, dass der Preis um 25 % gestiegen ist.

Anwendungsbereiche im Alltag und Beruf

Der prozentuale Unterschied ist in vielen Bereichen unverzichtbar:

• 🛍️ Einkauf: Preissteigerungen oder Rabatte verstehen.
  
• 📈 Finanzen: Gewinn- und Verlustrechnungen interpretieren.
  
• 📊 Statistik: Veränderungen in Bevölkerungszahlen, Arbeitslosenzahlen oder Marktanteilen erkennen.
  
• 🧠 Bildung: Notenverbesserungen oder -verschlechterungen auswerten.
  

Durch die Berechnung des prozentualen Unterschieds lassen sich Entwicklungen besser bewerten und fundierte Entscheidungen treffen.

Formel zur Berechnung des prozentualen Unterschieds

Um den prozentualen Unterschied zwischen zwei Zahlen zu berechnen, gibt es eine einfache, standardisierte Formel. Sie hilft dabei, die relative Veränderung schnell und präzise zu bestimmen.

Standardformel

Die allgemeine Formel lautet:

Prozentualer Unterschied = (Neuer Wert – Alter Wert) ÷ Alter Wert × 100

Oder kompakt formuliert:

% Unterschied = (Δ Wert ÷ Alter Wert) × 100

Beispiel:

• Alter Wert = 80 €
  
• Neuer Wert = 100 €
  

Berechnung:

(100 – 80) ÷ 80 × 100 = 25 %

Alternative Formeln bei negativen Werten oder Rückgängen

Wenn der neue Wert kleiner ist als der alte Wert (z. B. bei Preisnachlässen oder Verlusten), bleibt die Berechnung identisch – das Ergebnis wird jedoch negativ interpretiert oder als Rückgang bezeichnet.

Beispiel bei Rückgang:

• Alter Wert = 100 €
  
• Neuer Wert = 80 €
  

Berechnung:

(80 – 100) ÷ 100 × 100 = -20 %

Das Minuszeichen zeigt einen Rückgang um 20 % an.

💡 Tipp: Oft wird das Minuszeichen weggelassen und stattdessen gesagt: „Der Wert ist um 20 % gesunken.“

Häufige Fehlerquellen und wie man sie vermeidet

• ❌ Falsche Bezugsgröße wählen: Immer den alten Wert als Referenz nehmen, nicht den neuen!
  
• ❌ Vergessen, das Ergebnis mit 100 zu multiplizieren: Ohne Multiplikation bleibt der Wert als Dezimalzahl stehen.
  
• ❌ Verwechslung von absolutem und prozentualem Unterschied: Immer klar trennen: absolute Differenz in Einheiten, prozentuale Differenz in Prozent.

Schritt-für-Schritt-Anleitung zur Berechnung

Damit du den prozentualen Unterschied zuverlässig bestimmen kannst, folgt hier eine einfache Schritt-für-Schritt-Anleitung. So vermeidest du typische Fehler und behältst den Überblick.

Schritt 1: Identifikation von altem und neuem Wert

Bestimme klar:

• Alter Wert = Ausgangswert, auf den sich die Veränderung bezieht
  
• Neuer Wert = aktueller Wert nach der Veränderung
  

Beispiel:
Ein Produkt kostete ursprünglich 200 €, jetzt kostet es 240 €.

Schritt 2: Anwendung der Formel

Setze die Werte in die bekannte Formel ein:

Prozentualer Unterschied = (Neuer Wert – Alter Wert) ÷ Alter Wert × 100

Berechnung:

(240 – 200) ÷ 200 × 100 = (40 ÷ 200) × 100 = 20 %

Schritt 3: Interpretation des Ergebnisses

• Ein positives Ergebnis zeigt eine Zunahme (z. B. Preiserhöhung, Gewinnsteigerung).
  
• Ein negatives Ergebnis zeigt eine Abnahme (z. B. Preisnachlass, Umsatzrückgang).
  

In unserem Beispiel:
→ Der Preis ist um 20 % gestiegen.

Praxisbeispiele für prozentuale Unterschiede

Um den prozentualen Unterschied richtig zu verstehen, helfen konkrete Beispiele aus dem Alltag. Hier zeigen wir typische Anwendungen und Berechnungen.

Preisänderungen bei Produkten

Beispiel:
Ein Fernseher kostet im Januar 500 €. Im März kostet er 450 €.

Berechnung:

(450 – 500) ÷ 500 × 100 = (-50 ÷ 500) × 100 = -10 %

Interpretation:

Der Preis ist um 10 % gesunken.

Gehaltsveränderungen

Beispiel:
Dein Gehalt steigt von 2.500 € auf 2.750 €.

Berechnung:

(2.750 – 2.500) ÷ 2.500 × 100 = (250 ÷ 2.500) × 100 = 10 %

Interpretation:

Dein Gehalt ist um 10 % gestiegen.

Veränderungen in statistischen Daten

Beispiel:
Die Einwohnerzahl einer Stadt sinkt von 120.000 auf 114.000.

Berechnung:

(114.000 – 120.000) ÷ 120.000 × 100 = (-6.000 ÷ 120.000) × 100 = -5 %

Interpretation:

Die Einwohnerzahl ist um 5 % gesunken.

Prozentuale Veränderung vs. prozentualer Unterschied

Obwohl die Begriffe prozentuale Veränderung und prozentualer Unterschied oft synonym verwendet werden, gibt es feine, aber wichtige Unterschiede. Verstehen wir beide Konzepte klar, vermeiden wir Missverständnisse bei Berechnungen und Analysen.

Definition der prozentualen Veränderung

Die prozentuale Veränderung beschreibt die relative Veränderung eines Wertes über die Zeit hinweg, bezogen auf seinen ursprünglichen Wert.

Formel:

Prozentuale Veränderung = (Neuer Wert – Alter Wert) ÷ Alter Wert × 100

Beispiel:
Ein Aktienkurs steigt von 50 € auf 60 €.

Berechnung:

(60 – 50) ÷ 50 × 100 = 20 %

Interpretation:

Der Kurs ist um 20 % gestiegen.

Vergleich beider Konzepte mit Beispielen

• Prozentualer Unterschied wird häufig bei Vergleichen zweier unterschiedlicher Werte verwendet (z. B. zwei Preise, zwei Bevölkerungszahlen).
  
• Prozentuale Veränderung betont dagegen die Entwicklung eines einzelnen Wertes über die Zeit.
  

Vergleichsbeispiel:

• Produkt A kostet 80 €, Produkt B kostet 100 €. → Prozentualer Unterschied: (100 – 80) ÷ 80 × 100 = 25 %
  
• Ein Produkt verteuert sich von 80 € auf 100 €. → Prozentuale Veränderung: (100 – 80) ÷ 80 × 100 = 25 %

Wann verwendet man welches Maß?

• 📈 Veränderung über Zeit: → Prozentuale Veränderung (z. B. Gehalt, Preise, Umsätze).
  
• 🔄 Vergleich zweier aktueller Werte: → Prozentualer Unterschied (z. B. Marktanteile, Preise zweier Produkte).
  

Tools und Rechner zur Unterstützung

Nicht immer möchte man prozentuale Unterschiede per Hand berechnen. Gerade bei komplexeren Aufgaben oder vielen Zahlen helfen digitale Tools, Zeit zu sparen und Fehler zu vermeiden.

Online-Rechner für prozentuale Unterschiede

Es gibt zahlreiche kostenlose Online-Rechner, die schnell und zuverlässig den prozentualen Unterschied ermitteln.
Du gibst einfach den alten und neuen Wert ein – das Tool übernimmt die gesamte Berechnung.

Empfohlene Tool:

Diese Rechner bieten oft zusätzliche Funktionen wie Diagramme oder eine grafische Darstellung der Veränderung.

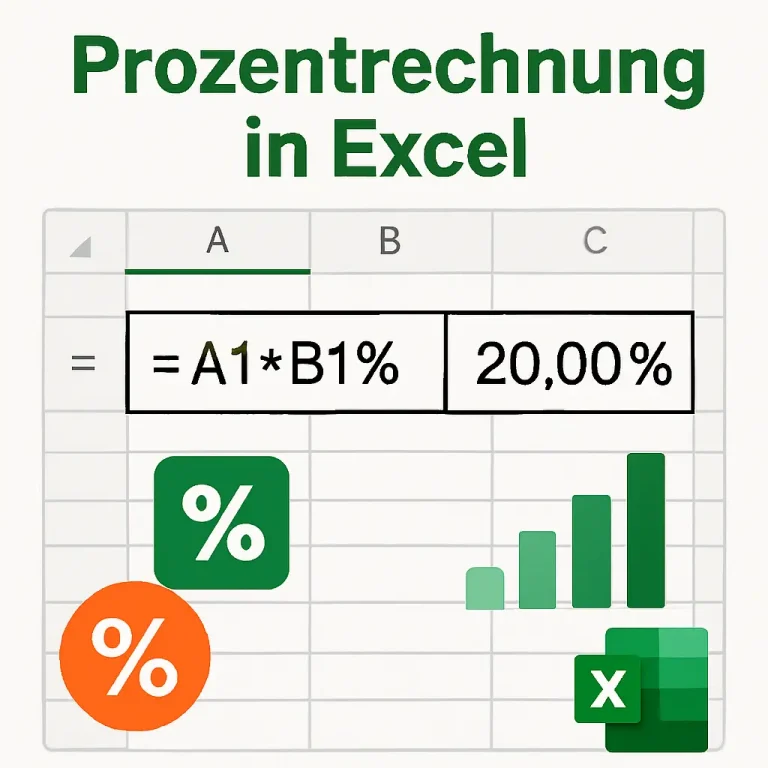
Excel-Formeln und -Funktionen

Für größere Datenmengen eignet sich Microsoft Excel perfekt.

Einfache Formel in Excel:

=(Neuer_Wert – Alter_Wert) / Alter_Wert * 100

Beispiel:

• Alter Wert in Zelle A1
  
• Neuer Wert in Zelle A2
  
• Formel in Zelle A3:

=(A2-A1)/A1*100

Excel kann große Tabellen automatisch durchrechnen und hilft, Trends oder Muster zu erkennen.

Mobile Apps und weitere Hilfsmittel

Für unterwegs gibt es auch praktische mobile Apps, die Prozentdifferenzen berechnen:

• Percent Calculator App (Android / iOS)
  
• All-in-One Calculator (umfangreiche Mathe-Tools)
  
• Calculator Plus (sehr einfache Bedienung)
  

Diese Apps sind nützlich beim Einkauf, in Besprechungen oder bei statistischen Analysen.

Häufige Fragen (FAQ)

Hier findest du Antworten auf häufige Fragen rund um die Berechnung des prozentualen Unterschieds. Diese Klarstellungen helfen dir, typische Unsicherheiten zu vermeiden.

Wie interpretiere ich negative prozentuale Unterschiede?

Ein negativer prozentualer Unterschied bedeutet, dass der neue Wert kleiner ist als der alte Wert.
Statt „minus 20 %“ sagt man meist einfach: „Der Wert ist um 20 % gesunken.“

Was tun bei sehr kleinen oder sehr großen Werten?

Bei extrem kleinen alten Werten kann schon eine kleine absolute Änderung zu einem sehr großen prozentualen Unterschied führen.
In solchen Fällen sollte die Interpretation immer im Kontext betrachtet werden, damit die Zahlen nicht irreführend wirken.

Wie gehe ich mit Prozentwerten über 100 % um?

Ein Ergebnis über 100 % ist völlig normal, wenn der neue Wert mehr als doppelt so groß ist wie der alte.
Beispiel:
Steigt ein Wert von 50 auf 150, beträgt die prozentuale Veränderung 200 %.

Fazit

Den prozentualen Unterschied zu berechnen ist eine unverzichtbare Fähigkeit, egal ob im Alltag, im Beruf oder in der Wissenschaft. Mit einer einfachen Formel lässt sich schnell erkennen, wie stark zwei Werte voneinander abweichen – und das unabhängig von ihrer absoluten Größe.

Ob Preisänderungen, Gehaltsentwicklungen oder statistische Trends: Der prozentuale Vergleich hilft dabei, Entwicklungen besser zu bewerten und fundierte Entscheidungen zu treffen.
Wichtig ist dabei stets, sauber zwischen absolutem Unterschied, prozentualem Unterschied und prozentualer Veränderung zu unterscheiden.

Mit der richtigen Formel, einem klaren Verständnis der Begriffe und ein wenig Übung wirst du Prozentdifferenzen schnell und sicher berechnen können!